The power of compound interest

“Compound interest is the most powerful force in the universe.” Some people attribute this phrase to Albert Einstein himself, although in reality its origin is not clear. But there is no doubt about its accuracy.
If there is one tool that can make a difference to your finances, it is compound interest. Thanks to this, your money will work for you and your savings will multiply little by little without you having to do anything except be patient and disciplined.
What is compound interest?
What exactly is compound interest? Something as simple as reinvesting the profits generated by your investment. That is why the simplest way to define compound interest is to compare it to simple interest.
Simple interest is always calculated on the same amount invested and never generates new interest. To understand it better, imagine that you have 1,000 euros that you invest at 10% per year. In one year you have earned 100 euros that you use to treat yourself. The following year you invest the same 1,000 euros again. What will your profit be? The same as the first year and it will continue to be the same year after year. That is how simple interest works.
What if instead of spending the money you reinvested it? That is what occurs in compound interest: instead of spending the 100 euros of profit, you keep it and add it to the capital invested, so instead of investing 1,000 euros, you invest 1,100 euros and the profit is no longer 100 euros, but 110 euros. That’s how compound interest works and here you can see its effect.
| Simple interest | Compound interest | |
| Initial investment in the first year | 1.000 € | 1.000 € |
| Profit first year | 100 € | 100 € |
| Initial investment second year | 1.000 € | 1.100 € |
| Profit second year | 100 € | 110 € |
| Total money earned (year 1 and 2) | 1.200 € | 1.210 € |
How to calculate compound interest (formula)
The concept of compound interest is simple, but the calculation is not so simple. The formula for compound interest is:
Cf = Ci (1+i)ⁿ
Where,
- Cf is final capital.
- Ci is initial capital.
- i is the interest rate.
- n is the time the investment is held.
To make this easier, you can calculate the compound interest of an investment in Excel with the XIRR Function.
How does compound interest affect your savings?
Compound interest is what makes your money really work for you and helps your savings grow exponentially.
The legend about the invention of chess tells that an Indian king wanted to reward its creator by letting him choose what his reward would be. The wise man answered that he only wanted one thing: a grain of wheat that would double in value for each square of the game he had invented, starting from the first one. It was as simple as that.
In the first square he would receive one grain of wheat, in the second two, in the third four, in the fourth 8, in the fifth 16, and so on. He did not need to continue with his explanation. The king agreed to his request: wheat corresponding to the 64 squares of the board with each square having double the amount of the previous one.
It was agreed, so the monarch ordered that the wheat the wise man needed be gathered. He could not. There was not enough wheat in the granaries of the kingdom to pay the man. Do you want to know how many grains of wheat were in the last square of the board? 18,446,744,073,709,551,615 or more than 18 trillion.
That, but on a smaller scale, is what compound interest can do for your savings. And getting an investment with an annual return of 100% year after year is also the stuff of legends.
A practical example: from 10,000 to 50,000 euros.
This is not to say that compound interest does not multiply your savings. A more realistic example will help you understand how it can help you achieve your financial goals.
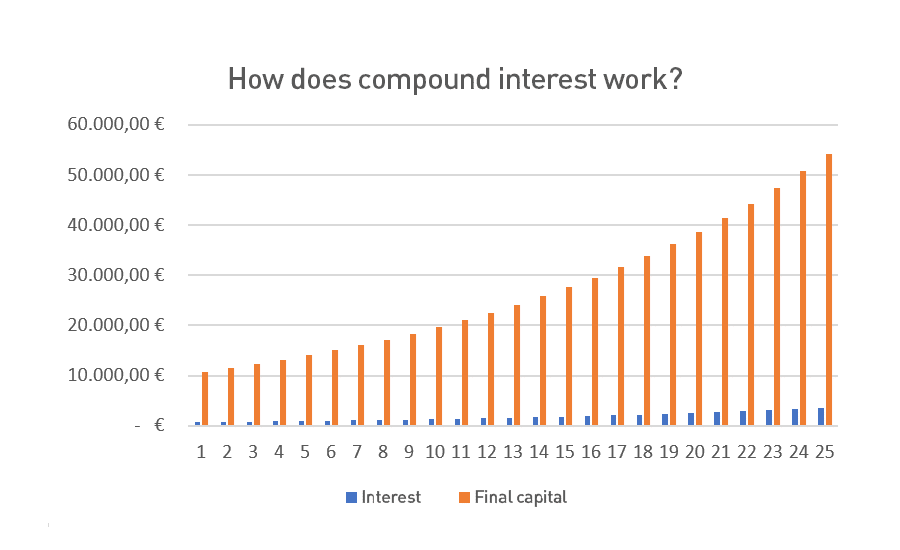
Imagine you have 10,000 euros and you invest them with an annual return of 7%. In the first year you would earn 700 euros. With compound interest, the profit in the second year would be 749 euros and your accumulated capital would be 11,449 euros. In the third year the interest would be 801.43 euros and the accumulated savings would be 12,250 euros.
What would happen if you left the money for 20 years? At the end of the period you would have 38,696.84 euros. And if you reached 25 years? Your capital would be 54,274.33 euros. Thanks to compound interest, the capital grows faster and faster due to the snowball effect.
It is like when you roll a snowball down a slope – it gets bigger and bigger with each turn. Just imagine that the snowball is your savings and the slope is interest and time.
5 keys to getting the most from compound interest
Is there a way to go faster? Is there a way to get more out of compound interest? Yes, there is. Just apply these five simple keys.
Add a little more each month
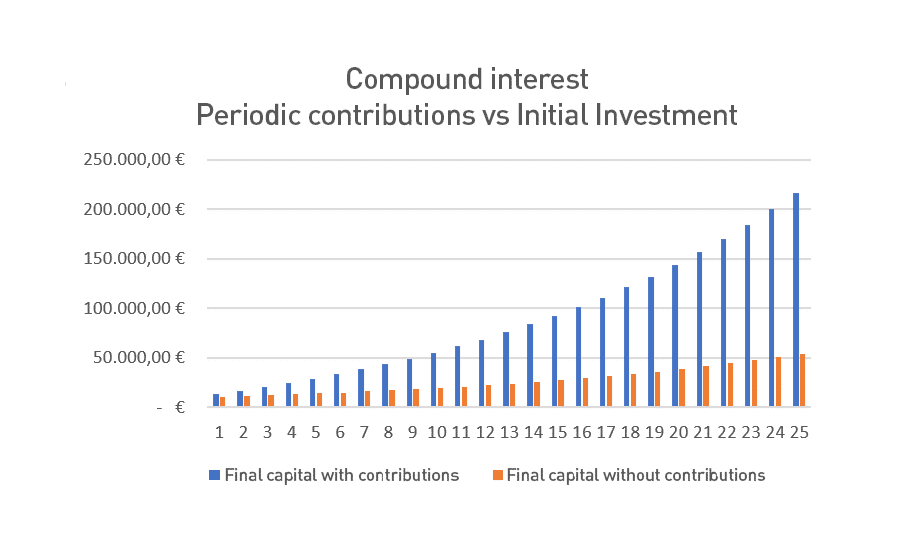
Compound interest rewards consistency. If, in addition to your initial savings, you add capital each month, the ball will grow much faster.
Let’s go back to the previous example. What would happen if to those initial 10,000 euros we add 200 euros of savings per month? As you can see in the following graph, the curve shoots up and so do the savings you get at the end.
Start as soon as possible
Compound interest only needs one thing to work: time. The longer you hold the investment and reinvest, the faster that snowball will grow.
To help you understand this better, imagine two friends: Juan and Pedro.
- Juan starts planning his finances when he is young. At the age of 23 he starts investing with an initial saving of 1,000 euros, to which he adds another 150 euros a month and maintains his plan until the age of 33 with a return of 7%.
- Pedro starts planning later. He starts at 33 and continues to save until retirement with the same return as Juan.
Which of the two will have more money saved by the time they are 65? The answer is Juan. Here you can see the difference and the savings effort made by each of them.
| Juan | Pedro | |
| Capital aportado | 19.000,00 € | 58.600,00 € |
| Intereses | 230.061,79 € | 162.395,44 € |
| Ahorro total | 249.061,79 € | 220.995,44 € |
As you can see, starting early pays off.
Interest also counts
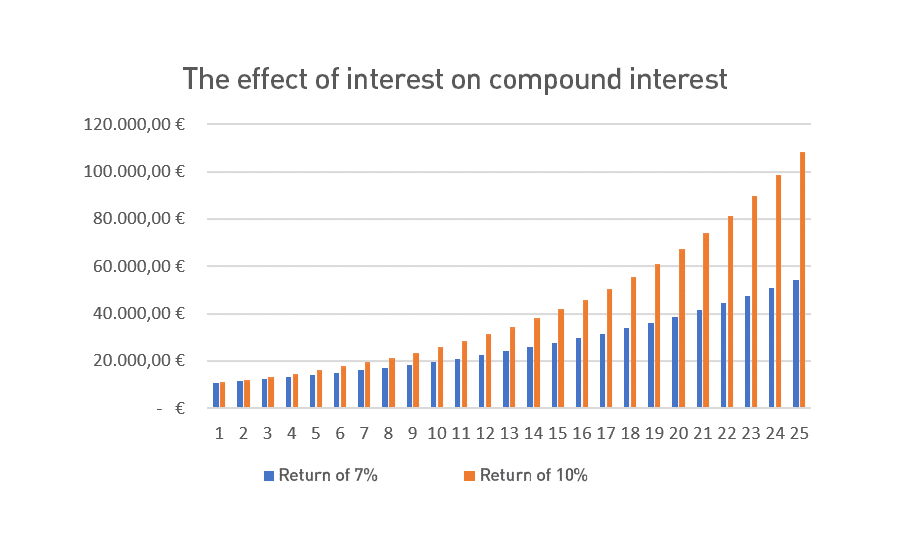
The interest you get for your money is also important: the difference between an annual return of 7% as in the example above and an annual return of 10% is enormous.
For an example like the one above of a starting investment of 10,000 euros, it means almost doubling the amount you will receive.
This is not to say that you should always take risks, only that it is a factor to be taken into account. When it comes to determining your profile as an investor, being able to sleep soundly is as important, if not more so, than the returns you get.
And taxes
Just as interest adds to compound interest, taxes take away. Each investment product works in a different way and has its own taxation rates.
To maximize compound interest, look for tax-deferred products. These are investments that allow you to delay the payment of taxes, so you do not have to pay between 19% and 26% of your annual profits each year to the Treasury when you make your income tax return.
Pension plans, PIAS and investment funds are three different ways to achieve this.
Perseverance
Finally, remember that compound interest needs time to work. It is a tireless force, but one that will require you to be patient until your snowball is big enough.
Combine these elements and you’ll be walking, then trotting, and finally running toward your financial and life goals. And all thanks to compound interest.


